栈:数据结构中的隐秘力量
1. 引言
栈(Stack)是计算机科学中一种基础而强大的数据结构,它以先进后出(Last In, First Out,LIFO)的方式管理数据。
2. 栈的基本概念
2.1 结构特点
栈是一种具有特殊操作规则的线性数据结构,它的主要特点是数据的存取遵循后进先出的原则。这意味着最后入栈的元素将首先被取出,而最先入栈的元素将最后被取出。
2.2 基本操作
- 入栈(Push): 将元素添加到栈的顶部。
- 出栈(Pop): 从栈的顶部移除元素。
- 栈顶(Top): 获取栈顶元素,不改变栈的结构。
- 栈空(IsEmpty): 判断栈是否为空。
- 栈大小(Size): 获取栈中元素的数量。
3. Python栈的实现
3.1 数组实现
使用数组作为底层数据结构是栈的一种常见实现方式。通过维护一个指针来跟踪栈顶的位置,实现栈的基本操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Stack:
def __init__(self):
self.items = []
def is_empty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
if not self.is_empty():
return self.items.pop()
def peek(self):
if not self.is_empty():
return self.items[-1]
def size(self):
return len(self.items)
|
3.2 链表实现
链表也可以用来实现栈,通过在链表的头部进行插入和删除操作,使得栈的操作更为高效。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class Stack:
def __init__(self):
self.top = None
def is_empty(self):
return self.top is None
def push(self, item):
new_node = Node(item)
new_node.next = self.top
self.top = new_node
def pop(self):
if not self.is_empty():
popped_item = self.top.data
self.top = self.top.next
return popped_item
def peek(self):
if not self.is_empty():
return self.top.data
def size(self):
current = self.top
count = 0
while current:
count += 1
current = current.next
return count
|
4. Java栈的实现

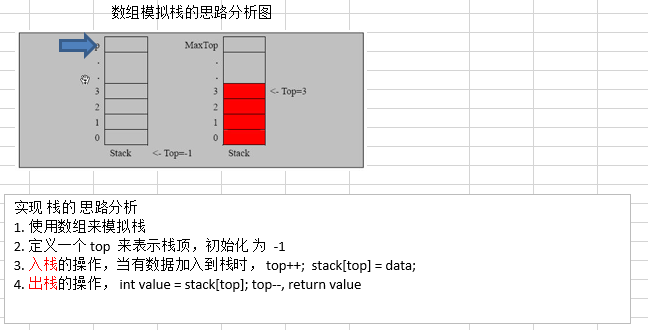
实现思路:
- 使用数组来模拟栈
- 定义一个top表示栈顶,初始化为-1
- 入栈操作,top++; stack[top] = data;
- 出栈,int value = stack[top] ; top – ; return value ;
4.1 数组实现
使用数组作为底层数据结构是栈的一种常见实现方式。通过维护一个指针来跟踪栈顶的位置,实现栈的基本操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
| package org.example;
import java.util.Scanner;
public class ArrayStackDemo {
public static void main(String[] args) {
ArrayStack arrayStack = new ArrayStack(10);
arrayStack.push(1);
arrayStack.push(2);
arrayStack.push(3);
arrayStack.push(4);
arrayStack.push(4);
arrayStack.list();
String key = "";
boolean loop = true;
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show:表示显示栈");
System.out.println("exit:表示退出栈");
System.out.println("push:表示添加数据到栈");
System.out.println("pop:表示从栈取数据");
System.out.println("输入选项:");
key = scanner.next();
switch (key) {
case "show":
arrayStack.list();
break;
case "exit":
scanner.close();
loop = false;
break;
case "push":
System.out.println("请输入一个数:");
int value = scanner.nextInt();
arrayStack.push(value);
break;
case "pop":
try {
int res = arrayStack.pop();
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
default:
break;
}
}
System.out.println("已退出");
}
}
class ArrayStack {
private int maxSize;
private int[] stack;
private int top = -1;
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
public boolean isFull() {
return top == (maxSize - 1);
}
public boolean isEmpty() {
return top == -1;
}
public void push(int value) {
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
public int pop() {
if (isEmpty()) {
throw new RuntimeException("栈空");
}
int value = stack[top];
top--;
return value;
}
public void list() {
if (isEmpty()) {
System.out.println("栈空");
return;
}
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
}
|
4.2 链表实现
链表也可以用来实现栈,通过在链表的头部进行插入和删除操作,使得栈的操作更为高效。
5. 栈的应用场景
5.1 函数调用
计算机程序中的函数调用过程就是一个典型的栈的应用场景。每次函数调用时,相关的信息被压入栈中,函数执行完毕后再弹出,确保程序执行的顺序和内存的正确管理。
5.2 表达式求值
在编译器中,栈常被用于表达式求值。通过维护操作数栈,可以有效地计算中缀表达式的值。
5.3 括号匹配
栈也常用于检查表达式中括号的匹配情况。通过在遍历表达式时将左括号入栈,遇到右括号时出栈,最后检查栈是否为空,可以判断括号是否匹配。
6. 总结
栈是一种简单而强大的数据结构,。通过先进后出的原则,栈不仅提供了一种高效的数据管理方式,还在函数调用、表达式求值、括号匹配等场景中展现了强大的实际应用价值。